Spini (1/2, 3/2, 5/2,...., yarım tam sayı) kere h/2 π değerlerinde olan elektron, proton gibi parçacıklara fermiyon dendiğini ve bunların Pauli Dışlama İlkesi’ne uyduklarını, yani iki özdeş fermiyonun aynı kuantum durumuna yerleştirilemeyeceğini söylemiştik. Spinleri (0, 1, 2, ...., tam sayı) kere h/2 π gibi değerler taşıyan piyon, foton gibi parçacıklaraysa bozon denilir; bunlarsa aynı kuantum durumuna yerleşmeye eğilimlidir. Böylece fermiyonlar arasında bir itme, bozonlar arasındaysa bir çekme etkisi doğar. İtme etkisinin maddenin uzayı doldurmasındaki rolüne değindik; bunun ötesinde beyaz cüce ve nötron yıldızlarının kütleçekiminin çekici etkisine direnerek çökmemelerini de Dışlama İlkesi sağlar. Bozonlardaki çekme etkisiyse lazerler, süperiletkenlik, süperakışkanlık gibi çarpıcı olaylara yol açar; bu olayları çarpıcı kılan, kuantum fiziğinin koherensle ilgili etkilerinin makroskopik ölçekte kendilerini gösterebilmeleridir.


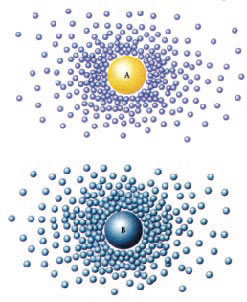
Boşlukta sanal A elektronu (üstte), zıt elektrik yüküne sahip sanal parçacıklar tarafından çevreleniyor, sanal bir kuark ise (altta) aynı renge sahip sanal kuarklar va gluonlar tarafından sarılıyor.

Spinin yarım ya da tam sayı olmasıyla parçacığın fermiyon ya da bozon özellikleri göstermesi arasında deneysel olarak gözlenen ilişkinin genel bir teorik açıklaması 1934-1958 arasında Pauli ve Burgoyne’ın makaleleri, Wigner’in Poincaré grubunun temsilleri hakkındaki çalışmalarıyla mümkün oldu. Açıklamamıza Wigner’in görüşleriyle başlayalım. Matematikte grup adı verilen yapı simetri operasyonlarından oluşur. Poincaré grubu da koordinat sistemlerinin uzayda döndürülmesi, bir yerden başka bir yere taşınması ve bir koordinat sisteminin, ona göre sabit hızla düz bir yönde hareket eden bir başkasıyla değiştirilmesi operasyonlarından oluşur. Simetriyle kastedilen de fizik yasalarının tüm bu koordinat sistemlerinde aynı olması, bu operasyonlar altında değişmemesidir; bu değismezlik zaten daha önce gördüğümüz gibi Einstein’in özel görelilik kuramıyla ortaya konmuştu. Wigner, grubun cebirinden her parçacık ya da bağlı olduğu alan için iki değişmez sayı olduğunu gösterdi: Parçacığın kütlesi ve spini. Gene cebirden kütlenin sürekli her hangi bir pozitif değeri, fakat spinin sadece yukarıdaki tam sayı ya da yarım tam sayı değerleri alabileceği çıkıyordu. Ayrıca Poincaré grubundan tamsayı spinli parçacıkların E ² =p ² c ² +m ² c ⁴ ilişkisine dayanan, buna karşılık elektron gibi yarım tamsayı spinlilerinse E=+ (p ² c ² +m ² c ⁴ )1/2 ve E=- (p ² c ² +m ² c ⁴ )1/2 ilişkilerine uyan denklemler sağlayacağı görülüyordu.

Artık bu bilgiler ışığında neden fermiyonların Pauli Dışlama İlkesi’ne gereksinim duyduklarını görebiliriz: Bu ilke olmasaydı ve istediğimiz kadar elektronu bozonlarla yapabildiğimiz gibi aynı düzeye koyabilseydik, negatif enerji düzeylerini doldurup pozitif enerjilere geçebilmek hiç mümkün olmayacaktı; tam bir dipsiz kuyuyla karşılaşacaktık. Öte yandan, bozonlara Dışlama İlkesi uygulandığındaysa, ışık hızını aşan sinyaller gönderme olasılığı gibi kabul edilemeyecek bir başka sonuç ortaya çıkacaktı.

Kuantum fermiyon alanlarının Dışlama İlkesine, bozon alanlarınınsa parçacıkların aynı durumda bulunmalarını sağlayan bir istatistiğe uymaları matematiksel şekilde şöyle ifade ediliyor: Ayrı uzay-zaman noktaları (x,y,z,t) ve (x’,y’,z’,t’)’de tarif edilmiş iki Alan operatörü (bunları uzay zamanın fonksiyonu olan devâsâ sonsuza sonsuz matrisler olarak düşünebiliriz) birbirleriyle önce biri sağda, öbürü solda olmak üzere, sonra da sıraları değiştirilerek çarpılıyor. Fermiyonlar için bu iki terimin arasına artı, bozonlar içinse eksi konulup ifadenin Planck sabitine orantılı bir fonksiyona eşitlenmesi gerekiyor. “Komütasyon bağıntısı” denen bu ilişkiler, hem kuramın kuantum özelliklerini, hem de artı ya da eksi işaretine göre fermiyon ya da bozon karakterini belirliyor. Aslında Heisenberg Belirsizlik İlkesi de konum ve momentum operatörleri arasında böyle bir ilişkiden çıkartılıyor; bu yüzden daha önce yoğun maddenin sıkıştırılamama özelliğinden söz ederken saydığımız iki nedeni bire indirebiliriz. Kuantum alanlar kuramında Heisenberg Belirsizlik İlkesi de, Dışlama İlkesi de Alan komütasyon bağıntılarının içinde.

Bilim ve Teknik Ekim 2010 düzenleme fizikciyiz.com

Henri Poincaré Fransız matematikçi, fizikçi filozof
http://tr.wikipedia.org/wiki/Henri_Poincar%C3%A9



Etiketler (pauli, fermiyon, planck, alan, kuantum, spin, istatislik, elektron, kuark, va, gluoni, dışlanma, )
Tarafımızca yazılan yazıların hakları saklıdır.

Benzer Başlıklar... » Lami Teoremi Sinüs Teorem

Henüz yorum eklenmemiş..2102

Türkçemizi katletmeden harf ve imlâ yapımıza uyacağınızı düşünüyoruz.
Uygunsuz içerikler savcılığa bildirilmek üzere kayıt altına alıyoruz.
21.11.2024, 12:31

Adınız
Yorumunuz

Her hakkı saklıdır.
Görüntüleme 5777