Maddeninn katı halinde belli bir şekle ve hacme sahiptir. Haliyle bu katı maddeniz atom ve molekülleri birbirine çok yakın olduğundan dolayı aralarında boşluklar oldukça azdır. Aslında bu durum katı maddenin atom ve moleküllerinde bir düzenlilik getirir.

Dayanıklılık hesabı yapmadan önce öncelikle geometrimiz iyi olmalıdır. Burda basitçe hacim ve yüzey alanın hesabını yapabilmeliyiz ki bu işlemler aslında ortaokul yıllarınızda zaten görmüşünüzdür.

Dayanıklılık, katı maddenin kendisine gösterilen kuvvete karşı göstermiş olduğu dirençtir.

Dayanıklık D ile Hacim V ve Kesit Alanı K.A ile gösterim yaparsak ;

D α K.A/V

DAYANIKLILIK α KESİT ALANI / HACİM

 

• Katı bir maddenin ayrıntılarında yani ebatlarındaki değişim maddenin hacminde, kesit alanında ve yüzey alanında değişmeler olacaktır.
• Bu değişikler maddenin dayanıklılığı orantılı bir şekilde artar ya da azalabilir. Sonuçta dayanıklılık dediğimiz durum maddenin;kesit alanı ile doğru orantılı, hacmi ile ters orantılıdır.
• Yani bir katı maddenin ebatlarını aynı oranda artırdığımızı düşünelim. Bu durumda bu katı maddenin dayanıklılığıda o oranda azalacaktır.
• Karıncayı düşünün, kendi ebatının kaç katını taşıyabildiğini.

Dayanıklık D ile Hacim V ve Kesit Alanı K.A ile gösterim yaparsak D α K.A/V

Örneğin, bir küpün boyutunu 3 katına çıkarırsak dayanıklığı üçte birine iner.Mesala karınca kendi ağırlığının on katını taşıyabilsin.

Eğer bu karınca kendi ebatlarının şuandakinden iki katı daha fazla olsaydı kendi ağırlığının 10 katını taşıyamazdı.

 

Cisim düzgün bir geometriye sahipse genel olarak hacim hesabı:

Hacim = Taban Alanı x Yükseklik olarak hesaplarız.

 

Tabii bütün cisimler böyle değildir.

Dikdörtgenler Prizmasın Hacmi:

Bütün ayrıntılarının çarpımı ile,
V = a.b.c

Kesit Alanı ise altan ya da üsten baktığınızda prizmaya basit bir dikdörtgen göreceksiniz haliyle iki ayrıntının çarpımı kesit alanını verir.;

K.A = a.b

Küpün her tarafı kara şeklindedir. Toplam 6 kare vadır. Burdan karenin alan hesabından toplam yanlanlarının toplamını bulabilirsiniz.

Küpün kesit alanında küpü kesin yukarda baktığınızı hayal edin. Karşınızda kare çıkar. O vakit küpün kesit alanı karanin alanıdır.

Küreyi tam ordan kestiğinizi hayal ediniz. Kesilen parçaya bakın karşınıza daire çıkar. Kürenin kesit alanı dairenin alanıdır.

gibi.. Aşağıdaki tablo gibi bir çok kitapta buna benzer şekiller vardır. Bunları mecburen bilmenizde fayda vardır.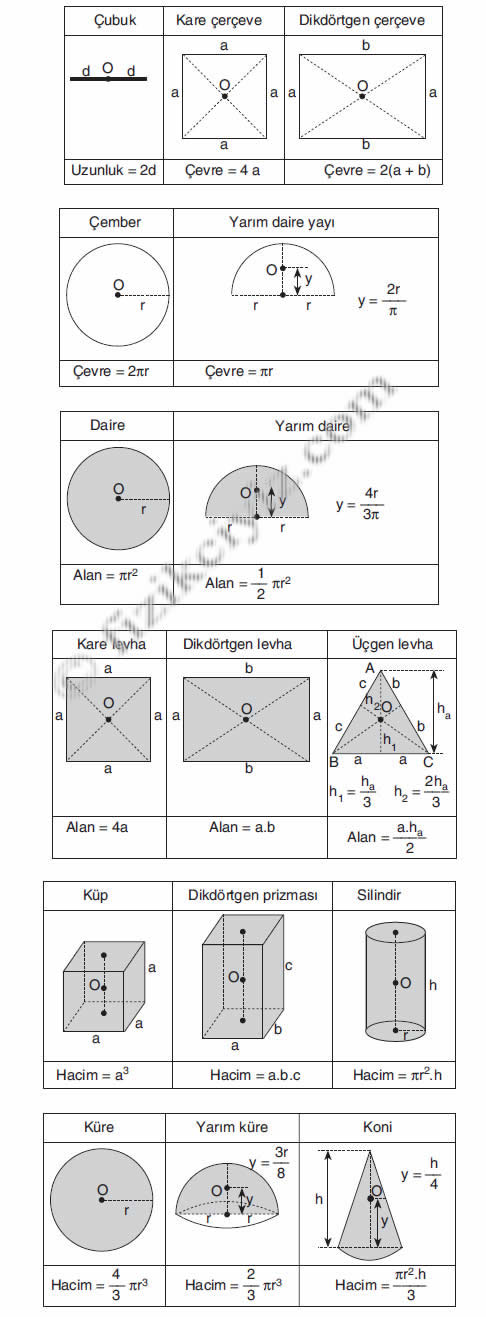

 

 

 

 

Göktuğ Serkan Bozoklu

Göktuğ S. Bozoklu / M.A (Fizik Öğretmeni)

Fotoğraflar (Sayfa 1)

Sayfalar o>>

Etiketler (kuvvet, katı, dayanıklılık, hacim, yüzey, alanı, direnç, )
Tarafımızca yazılan yazıların hakları saklıdır.

Benzer Başlıklar...

Yorumlar (9)2952

1. evren [03.12.2016, 21:09 ]

   ?

   Konuyu bir türlü bulamiyorum

2. jjdjfnbkgdşlnk [04.12.2016, 20:11 ]

   ?

   bende bulamıyorumbirsayfada bile olmazmı ya allahım
   allah belasını versin böyle konunun ve böyle bir dersin ve böyle bir okulun :8 :( :( ::((((:8:8:8(:(:(:(:8:((:(:((:(:(:(:8:(

3. dsjfosjfdjofdfdfd [18.12.2016, 13:24 ]

   ?

   saddasdasd

4. FATMA nur [27.12.2016, 18:29 ]

   ?

   çok saol :)

5. Deniz Kumlu [08.11.2017, 21:41 ]

   ?

   HIHIHA İŞTE BU

6. mustafa talaş [28.11.2017, 21:02 ]

   ?

   çok zor buldum ama deydi teşekkürler

Türkçemizi katletmeden harf ve imlâ yapımıza uyacağınızı düşünüyoruz.
Uygunsuz içerikler savcılığa bildirilmek üzere kayıt altına alıyoruz.
21.11.2024, 10:28

Adınız
Yorumunuz

Her hakkı saklıdır.
Görüntüleme 25107