VEKTÖR İŞLEMLERİ
TEMEL BECERİLER

Fizik, deneye ve ölçmeye dayalı bir bilim dalıdır. Haliyle kafamıza göre varsayımlar,önergeler ya da yargılarda bulanamayız.

Ölçümleri ifade etmek için kullanılan en basit ve genel dil sayılardır.

Kütle, hacim, uzunluk, sıcaklık, enerji gibi fiziksel büyüklükleri tanımlamak için onların sayısal değerini ve birimini bilmek
gerekli ve yeterlidir.Bunlar için doğrultu ya da yön bilgisine gerek olmadığı gibi anlamlıda olmaz.

Örneğin; Kuzey yönünde 50 kg gibi saçma bir cümle kuramayız.

Bu durumdaki büyüklüklere skaler büyüklükler denir. Basit bu fiziksel nicelikler sadace sayı sembol ve birim ile ifade edilir.

Hız, kuvvet, ivme gibi fiziksel büyüklükleri tanımlamak için onların sayısal değerleri ve birimiyle birlikte doğrultu ve yönünün
de bilinmesi gerekmektedir. Bu durumdaki büyüklüklere vektörel büyüklüklerdenir.

Örneğin; Ankara'dan Samsun'a 50 km/h hızla gidiyorum derken, yönümü belirterek hız vektörümün yönünü belirtiyorum

Başlangıç noktası, şiddeti, birimi, yön ve doğrultusu olan büyüklükler vektöreldir.

• Bir vektör, vektörün sembolünün üzerine bir ok çizilerek gösterilir. Ok ilgili vektör ya da kuvvetin üzerine eklenir. Eğer eklenmezse bu skaler kabul edilir ve işlemleri tamamen değiştiren bir durum ortaya çıkar. Örneğin A bir vektör ise kesinlikle üzerine ok işareti konulmalıdır.

 

Örneğin;
                →
Hız vektörü V
                        →
Kuvvet vektörü F

ile tanımlanır.

• Bir vektör, yönlendirilmiş doğru parçasıyla gösterilir. Şiddeti boyu ile doğru orantılıdır.

Her bir vektör, vektörün büyüklüğünü ve yönünü gösteren bir okla gösterilir.

Yönü ve şiddeti aynı olan vektörlere eşit vektörler denir.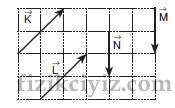

Üsteki vektörlerden K ile L ve M ile N vektörler eşit vektörlerdir.

Bir vektörün yönü bilindiğinde doğrultusu da bilinir. Doğrultusu bilindiğinde yönü için kesin birşey söylenemez. Çünkü her doğrultu için, birbirine zıt iki yön vardır.
→
K ile gösterilen bir vektörün yönü ters çevrildiğinde, bu vektör
 →
–K  şeklinde gösterilir.

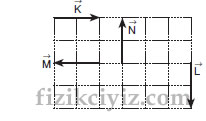
Anlaşılacağı üzerine - işareti burda ters anlamındadır. Hiç bilmeyen için ; Basitçe başlangıç ve bitiş noktaları birbirleri arasında yer değiştirirseniz ters ortaya çıkar.

Şiekilde verilen vektörler arasında
→     →
K = – M
→      →
N = – L

eşitliğini yazabiliriz.

 

Bir vektör, büyüklüğü ve yönü değiştirilmeden başka bir yere taşınabilir. Zaten taşıma işlemi yapamazsak vektör işlemlerini yapamayız.

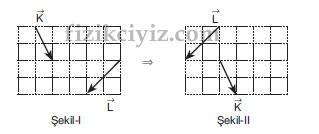
Şekil 1 ki K ve L vektörlerini şekil 2 deki gibi kolayca taşıyabiliriz.

Herhangi bir vektör ile skaler çarpılabilir. Elde edilen büyüklük de bir vektördür. İstediğimiz skalerle işlem yapabiliriz. Ortaya çıkan sonuç yine vektör olacaktır.

 

Şekildeki vektörler için;
K = 2M

lKl = lNl

L= 3/2 N

 lLl = 3lMl

gibi, çarpma ve bölme işlerimlerini yukardaki gibi yaparız.

Bir vektör, herhangi bir koordinat sisteminde bileşenlerine ayrılabilir.-ki bu işlemler kuvvetten, momente yani torkayani dönme kuvvetine kadar, dairesel hareketten harmaniğe kadar bileşen ayırma işlemini kullanırız. Buna benzer işlemler temel okur yazarlık gibi olmaldır.

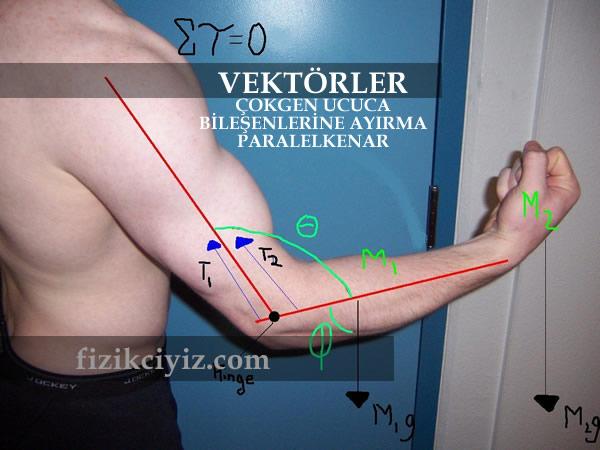
VEKTÖRLERİN TOPLANMASI
                                                                                                          →
Birden fazla vektörün toplanmasıyla elde edilen vektöre bileşke vektör denir. R ile gösterilir

Örneğin;

→    →
K ve L  vektörlerinin toplamı

→    →  →
R = K + L  olarak yazılır.

• Vektörlerin toplanması skalerlerin toplanmasından farklıdır.

Örneğin;

Skaler büyüklük

VK = 3 m/s V
VL = 4 m/s V

Skaler büyüklüklerin toplamı
VK + VL = 7 m/s bulunur.

 

Vektörel Büyüklük

K = 3 m/s, kuzey

L = 4 m/s, doğu

Vektörel büyüklüklerin toplamı
VK + VL = 7 m/s bulunmaz. Çünkü vektörler yünlü büyüklüklerdir.

Vektörlerin toplanmasında geometrik ve analitik yöntemler kullanılır. Çünkü vektörler yönlü büyüklüklerdir.

Bu yöntemler,

l. Paralelkenar
ll. Çokgen (Uç Uca Ekleme)
lll. Bileşenlere Ayırma diye adlandırılır.

PARALELKENAR YÖNTEMİ

İki vektörün toplamı hesaplanırken bu yöntemde, iki vektörün başlangıç noktaları çakıştırılır. Her bir vektörün ucundan diğer vektöre paralel çizilir. Başlangıç ile paralellerin kesiştiği noktalar birleştirilir.

Elde edilen şekil paralelkenardır. Paralelkenarın köşegeni

→
R ,bileşke vektörüdür.

ÇOKGEN (UÇ UCA EKLEME) YÖNTEMİ

Vektörlerin yönleri ve şiddetleri değiştirilmeden birinin bitiş noktasına diğerinin başlangıç noktası gelecek şekilde uç uca eklenmesi sonucu bileşkenin büyüklüğünün hesaplandığı yöntemdir.

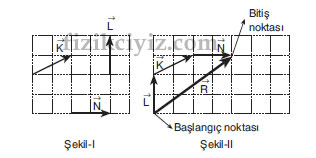
Şekil - l deki K, L, N vektörlerinin bileşkesini bulmak için Şekil - ll ye taşırken herhangi bir başlangıç noktası seçilmiş ve vektörler uç uca gelecek şekilde eklenmiştir. Vektörler hangi sırayla eklenirse eklensin bileşke vektör değişmez, vektörlerin toplanmasında değişme özelliği vardır.

Bileşke vektör, başlangıç noktası ile bitiş noktası birleştirlerek elde edilir.

İkiden fazla vektörün bileşkesi bu yöntemle daha kolay bulunabilir.

 

BİLEŞENLERE AYIRMA YÖNTEMİ

Her bir vektörün x ve y eksenine göre bileşenleri bulunur.
Vektörlerin bileşkesi R , x eksenindeki bileşenlerin bileşkesi RX,
y eksenindeki bileşenlerin bileşkesi RY dir.

 

ÖZEL DURUMLAR

 

 

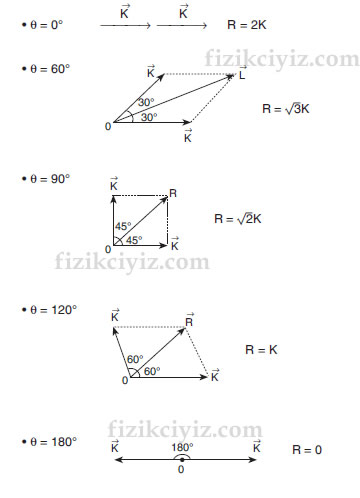
Bu değerler incelendiğinde bileşke vektör hakkında bazı yargı lara ulaşılır.

• θ = 0° olduğunda bileşkenin sayı değeri en büyük olur.

• θ = 180° olduğunda bileşkenin sayı değeri en küçük olur.

• Bileşkenin alabileceği değer iki vektörün toplamından büyük,farkından küçük olamaz.

• Bileşkenin sayı değeri vektörler arasındaki açı büyüdükçe küçülmektedir.

• Vektörlerin büyüklükleri eşit ve θ açısının değeri ;

0°< θ < 180° arasında ise bileşke vektör açıortay doğrultusundadır.

• Vektörlerin büyüklüğü farklıysa, bileşke vektör, büyük olana daha yakındır.

Vektör Videoları

"Vektör" Örnek Sorularda toplam 7 sayfa .

1-->> Kuvvetler ve Kesişen Kuvvetlerin Bileşkesi

2-->> Vektörler

3-->> ÖSS Vektörler Kuvvet Çıkmış Sorular

4-->> Vektörler II

Diğer vektör içerikleri için dokun!

 

Göktuğ Serkan Bozoklu

Göktuğ S. Bozoklu / M.A (Fizik Öğretmeni)

Fotoğraflar (Sayfa 1)

Sayfalar o>>

Etiketler (vektör, bileşke, çokgen, ucuca, paralelkenar, )
Tarafımızca yazılan yazıların hakları saklıdır.

Benzer Başlıklar... » Skaler ve Vektörel Büyüklükler » Hareket Nedir? » Fizik Nedir? Fizik Alanları Nedir? » Vektörler ve Kuvvet » Hidrofobik ve Hidrofilik Yüzey Nedir? » Vektör Konusunu Bir Ders Saatinde Örnek Anlatımı » Vektör Toplama (ikili) » İki Vektörün Bileşimi » Vektörler, Bileşke

Yorumlar (96)3002

Türkçemizi katletmeden harf ve imlâ yapımıza uyacağınızı düşünüyoruz.
Uygunsuz içerikler savcılığa bildirilmek üzere kayıt altına alıyoruz.
21.11.2024, 10:25

Adınız
Yorumunuz

Her hakkı saklıdır.
Görüntüleme 43748