- 10. Sınıf Fizik Konuları
- 11. Sınıf Fizik Konuları
- 12. Sınıf Fizik Konuları
- 9. Sınıf Fizik Konuları
- Atışlar
- Atom Fiziği
- Aydınlatma
- Bağıl Hareket Nehir Problemleri
- Basınç
- Basit Harmonik Hareket
- Basit Makineler
- Bilgiler
- Dalgalar
- Dinamik
- Doğrusal Hareket
- Düzgün Dairesel Hareket
- Düzlem ve Küresel Aynalar
- Elektrik
- Elektrik Akımı
- Elektromagnetik
- Elektrostatik
- Fiziğin Doğası
- Fizik
- Fizik Öğretimi
- Fizik Öğretmeni
- Fizik Simülasyonları
- Gölge
- Haber
- Hesaplamalar
- Isı ve Sıcaklık
- Işığın Kırılması ve Renk
- Işık
- İş Güç ve Enerji
- İtme Momentum Açısal Momentum
- Kuvvet Denge
- Kütle Ağırlık Merkezi
- Kütle Çekimi ve Kepler
- Lambalar
- Alan Yeterlilik Sınavı AYT
- Madde ve Özellikleri
- Manyetizma
- Mekanik
- Mercelekler
- Modern Fizik
- Modernfizik
- Moment - Tork- Dengesi
- Nükleer Fizik
- Optik
- Periyodik Hareketler
- Sıvıların Kaldırma Kuvveti
- Vektörler
- Temel Yeterlilik Sınavı TYT
Güncelleme / Ekleme :28/10/2008
Amaç: Vektörlerin yön ve doğrultusunun ve vektörlerin toplanmasını öğrencilere kavratmak.
Önerilen Süre:1 ders süresi
Öğretim Yöntemleri: Soru cevap, Düz anlatım, Tartışma, Problem çözme yöntemi
Önerilen kaynaklar: Temel Fizik Cilt II Arkadaş Yayınevi, ÖSS Fizik X Yayınları
Öğrencilere vektörlerin nasıl ve hangi yöntemlerle toplandığı anlatılır. Kısaca paralelkenar, çokgen, üçgen yöntemi gibi değişik yöntemlerle bulabiliriz
1. Yol: Öğretmen soruda sorulmak isteneni öğrencilere anlatır.1soruda önce verilenler
Dikkate alınırsa bize K-M vektörleri verilmiştir. Öğrencilere bir vektörün nasıl ters çevrileceği sorulur. Ardından iki vektörün çıkarılmasının nasıl yapılabileceği sorulur. Bu sorular cevaplandığında artık öğrenci soruyu çözmeye hazır hale gelmiştir. Öncelikle verilen vektörler paralel kenar yöntemi ile toplamak için iki vektörün uygulama noktaları aynı olacak şekilde bir noktaya taşınır. K-M vektörü ile K vektörü toplanır. Ancak burada K vektörü ters çevrilir. Ters çevirme işleminde K vektörünün sadece yönü değişir.
| ||||
K-M | ||||
| -K |
| -K |
|
| |
KM | ||||
-M | ||||
| ||||
L |
|
| |
K |
| ||||
L+M |
| |||
| ||||
|
Yukarıdaki şekillerde olduğu gibi paralel kenar yöntemi kullanılarak L+M bileşke vektör bulundu.
2. Yol: iki vektör üçgen yöntemi ile de toplanabilir. Üçgen kuralı ile toplamak için vektörlerden birinin uç noktasına diğerlerinin başlangıç noktası gelecek şekilde var olan vektörler eklenerek toplanır.
|
|
| |||||
| K-M | ||||||
L+M |
| -K | |||||
Yukarıdaki şekilde görüldüğü gibi öğretmen önce K+M vektörü ile K vektörünü uç uça ekleme metodu ile toplayıp ardından elde edilen M vektörünü ters çevirerek +M vektörünü elde eder. Bundan sonra yapılacak işlem öğretmenin öğrencilerine L ile M vektörlerini kimin toplayabileceği sorusunu sorması ve çözümün yapılıp yapılmaması halinde yine uc uca ekleme yöntemi ile bileşke vektörün bulunmasıdır.
3. Yol: Burada öğretmen bu yolu da öğrencilerine göstermelidir. Bu yöntem hem daha kolay hem de zaman bakımından daha tasarrufludur.
VEKTÖR | Yatay Bileşen | Dikey Bileşen(y) |
K-M | 1 | -2 |
-K | -2 | -1 |
R=-M | -1 | -3 |
+M | 1 | 3 |
L | -1 | -1 |
R=L+M | 0 | 2 |
Yukarıda ki tabloda her bir vektörün yatay ve düşey bileşenleri her bir birim kareye bir birim karşılık gelmek şartı ile bileşenlerin değerleri tabloya yazılır. Ardından bu problem için istenenler öğrencilere sorular sorularak sonuç öğrencilere buldurulur.
Etiketler (öğretmen, öğretim, stajer, öğrenci, üniversite, )
Tarafımızca yazılan yazıların hakları saklıdır.
Yorumlar (1)922
-
duru [27.09.2016, 19:02 ]
?Keşke bir kaç tane örnek soru olsaydı konu daha iyi anlaşılırdı...
Türkçemizi katletmeden harf ve imlâ yapımıza uyacağınızı düşünüyoruz.
Uygunsuz içerikler savcılığa bildirilmek üzere kayıt altına alıyoruz.
12.02.2025, 18:22
Her hakkı saklıdır.
Görüntüleme 7330


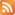




 M
M