Denge şartlarında olay basittir. Bu sayfadaki denge şartlarımız genel olarak çıkan/çıkabilen/sorulabilen soruların şemaları. Özellikle küre ve tepki kuvveti olan sorularda amacımız şekli karışıklıktan kurtarıp temize çekmektir. Temiz olayımız aslında lami teoremini uygulayabilmektir. En basit şekillerden başlayarak denge  şartlarını ve yeri geldikçe lami teoremini uygulayacağım aşağıda.

Denge şartında zıt yönlü kuvvetlerin büyüklükleri eşittir. Örneğin aşağı yönlü kuvvetlerin toplamı ile yukarı yönlü kuvvetlerin toplamına eşit olacaktır.

 

1- İp ve Küre

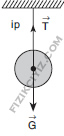
Aşağı yönlü ağırlığımız var yukarıda sadece T ip gerilmesi var. Denge şartı;

G = T_ip

2- İp ve Kaldırma Kuvveti

 

Fk dediğimiz kaldırma kuvvetidir. Denge şartı;

Fk = G + T

 

3- 3 İp ve Ağırlık

 

Denge koşulumuz;

 

T₁ + T₂ + T₃ = 0

T₃ = G

T₁ ve T₂ 'nin düşey bileşenlerinin toplamıda T₃ gerilmesine eşittir.

 

4-İp,Ağırlık ve F Kuvveti

T + F + G = 0

Yine T ip gerilmesini bileşenlerine ayıralım;

θ açısına göre ;

Tsinθ = F

Tcosθ = G

 

5-Çoklu ip gerilmesi

T₁+T₄+T₃= 0
T₂+T₃+T₅= 0
G1 = T4
G2 = T5

İplerin bağlandıkları noktalardaki açılar verilirse lami ile de sorular çözülür.T3 her iki taraf içinde aynıdır. Sağ ve sol taraf için ayrı ayrı lamide hesaplnabilinir.

 

6-Sabit makaradaki ip

T = G

Sabit makarada adı üstünde makara sabittir. Yani makaranın ağırlığının ipe bir etkisi yoktur. Bu tür durumlarda sistem dengede ise ipin her hangi bir noktasındaki gerilme kuvvetleri aynıdır.

 

7-Dikdörtgen düzlem iki sabit makara sistemi

 

Dediğim gibi ipin herhangi bir noktasındaki gerilme aynıdır.

T = G

 

*** ÖNEMLİ! ***

 Bir yüzey üzerinde duran cisimle, yüzey arasında cismin ağırlığından dolayı kuvvet oluşur. Bu kuvvete N tepki kuvveti denir. Yönü yapılan etkiye zıt, değeri-büyüklüğü- aynıdır. Bu bildiğimiz Newton Kanunlarının üçüncüsü, yani Dinamiğin III. Yasası: Etki-Tepki Kanunu

 

8-Ağırlık-Tepki Kuvveti

 

G = N 'dir.

 

Burada cismin ağırlığı G etkiyen kuvvet, N ise tepki kuvvetidir. Yönleri farklı ancak büyüklükleri eşittir.

 

9-Sürtünmeli düşey düzlem üzerinde kuvvet etkisiyle duran küre.

 

 

F = N

 N: Yüzeyin cisme uyguladğı tepki kuvveti.

 

10-Düşey ve yatay düzlem ekseninde tek küre

 

 

N₂ = G

N: Yatay yüzeyin cisme uyguladığı tepki kuvveti.

 

11- Düşey düzlemde küreyi tutan ip sistemi

 

 

 

T + N + G = 0

Yine T ip gerilmesini bileşenlerine ayıralım;

θ açısına göre ;

Tsinθ = F

Tcosθ = G

Burada iç dış açıdan açıları yerleştirebilirseniz lamiden de soruyu kolayca yapabilirsniz.

 

12.Tek bir küre açılı iki yüzey arasına oturtturulmuş.

 

N₁ + N₂ + G = 0

 

İkinci şekilde göreceksiniz ki şekli temize çektik. Lami uygulayabilecek konuma getirdik. Bu arada biliyorsunuz ki kuvvetleri taşıyabiliyoruz. Vektörler konusunda ilk girişte işlenmiştir. Karışık gelen ilk şekildeki önce küreye etkiken kuvvetleri tespit ediyoruz. Sonrasında temiz bir yere çiziyoruz.

 

Küre arkadaşımıza etiken üç kuvvette O noktasında geçtiğine göre, ben bunları bu noktayı merkez alacak şekilde lami teoremini uygulamak için çizerim. Kuvvetleri aynen taşıdığımızda soru kısa sürede çözülür.

Burda illa lamiden gidilecek diye bir kaide yok. Bileşenlerine ayırarak kuvvetleri zıt yönde olanları birbirne eşitleyebiliriz.

N₂ 'nin yatay bileşeni N₁ kuvvetine, düşey bileşeni G ağırlığına eşittir.

90 - θ = α dersek.

N₂.sinα = N₁

N₂cosα = G

olur.

 

13.İki yüzey arasına sıkışmış küre

 N₁+ N₂+G =0

Yine bileşen oalyı 12'deki durum gibi aynen uygulanabilinir.

 

14-İple yanyana asılmış iki küre.

 

 

 

T₁ = T₂ =T
G = T. cos α
N₁ = N₂

Küreler özdeş ve G ağırlında. İkizkenar üçgen oluşmuş. α açısına göre T'lerin yatay bileşenleri G ağırlığına eşit olur.(Aşağı kuvvetler = Yukarı Kuvvetler)

 

15-

 

 

GÖKTUĞ SERKAN BOZOKLU

Göktuğ S. Bozoklu / M.A (Fizik Öğretmeni)


Etiketler (vektör, küre, ip, gerilme, kuvvet, ağırlık, tepki, küreler, yüzey, düşey, yatay, duvar, lami, teorem, )
Tarafımızca yazılan yazıların hakları saklıdır.

Benzer Başlıklar... » Vektör nedir? » Kuvvet, keşişen kuvvetlerin dengesi » Deney , bağımlı , bağımsız ve sabit değişkenler » Skaler ve Vektörel Büyüklükler » Düzgün Doğrusal Hareket ve İvme » Öğretmenler için yılsonu işlemler, ders kesim raporu, yazılı kağıtları teslim tu » Basit Makinaler: Bölüm II; Palanga, çıkrık, dişli, kasnak ve vidalar » Lami Teoremi Sinüs Teorem » İlk hızlandırıcı laboratuarımız kanser için açıldı

Yorumlar (2)3082

1. Deniz Kumlu [28.01.2016, 16:24 ]

   ?

   YGS-LYS lik olmuş süperrrr

2. Gamze [28.01.2016, 18:28 ]

   ?

   Örnek soru var mı acep...

Türkçemizi katletmeden harf ve imlâ yapımıza uyacağınızı düşünüyoruz.
Uygunsuz içerikler savcılığa bildirilmek üzere kayıt altına alıyoruz.
21.11.2024, 13:12

Adınız
Yorumunuz

Her hakkı saklıdır.
Görüntüleme 17366