Bu harekette ivmesiz bir hareketimiz vardır. Önce ivmeyi tanımlayalım.

İvme:
Birim zamandaki hareketlinin hızındaki değişimdir. Değişimden kasıt hareketli/cisim hareketi boyunca hızını düşürebilir ya da artırabilir.

Örneğin arabamızın hızını önce 0 dan 100 km/h sonra 80 km/h 'a  indirelim. Bu çıkış ve inişler birer değişimdir. İşte ivme dediğim kavram, bu hızdaki artış ya da azalışlardır.Başka bir örnek verelim salıncakta ileri geri salınım yaparken hızımıda artış ya da azalışlara olacaktır. İşte bu zaman dilimindeki hızımızın değişimi ivmeyi ifade eder.

İvme;

- İnglize acceleration kelimesinin baş harfi "a" ile gösterilir.
- Büyüklüğü;

a = v/t  yani, İvme = Hız / Zaman

- Birimi ise; hızın birimi "m/s", zamanın birimi "s" olduğuna göre formülde birimleri yerine koyalım.
a = [m/s]/s = m/s² olur. Bu durumda ivmenin birimi m/s² dır.
- Vektörel bir büyüklüktür.
- Pozitif ya da negatif olabilir. Bu durum hızlandığımız ya da yavaşladığımızı gösterir.
 -Hızın yönü pozitif ise ivme de pozitiftir.
- Hızın yönü negatif ise ivme de negatiftir.

* Eğer hareketlinin ivmesi sabit ise hızı düzgün değişiyor demektir. İvmesi sıfır ise hareketlinin hızı da sabit (sbt) demektir.

Doğrusal Hareket Çeşitleri

Düzgün Doğrusal Hareket

Hareket süresince cismin hızının büyüklüğü sabittir. Hızı sabit olduğu için ivmesinin büyüklüğü sıfırdır.


DOĞAN S marka aracımız A şehrinden B şehrine V sabit hızıyla gitmektedir. Bu aracımız A'dan B'ye sabit bir hızla gelmiştir. Yani Düzgün Doğrusal Hareket yapmıştır. Hızında bir değişiklik olmadığı için ivmesi sıfırdır.

V = sabit => a = 0 (sıfır)

Cismin yer değiştirmesi;

X = V.t şeklinde ifade edilir.

Yol =  Hız x Zaman

X: Yerdeğiştirme miktarı (m)
V: Cismin hızının büyüklüğü (m/s)
t: Hareket süresi (s)

Hareket eden cismin grafiklerini yorumlayalım...

 

İlk grafikte, hareketlinin hızı sabit olduğu cisim birim zamandaa aldığı yollarda aynıdır.

Ortadaki grafikte cisimin hızının sabit olduğunu görüyoruz.

Son grafikte ise cismin hızının sabit olduğu için ivmesinide sıfır olduğunu görüyoruz.

ÖNEMLİ: Bir hareketlinin konum denkleminin zamana göre birinci türevi hızı ikinci türevi ise ivmeyi verir.

Buna göre, hız denkleminin zamana göre birinci türevide ivmeyi verir.

Tersinden gidecek olursak ivmedenkleminin zamana bağlı integralini alırsak hız denklemini, hız denkleminin zamana bağlı integralini alırsakta konum denklemini elde ederiz.

Bu ifadeye göre,

Konum - zaman grafiğinin eğimi bize hızı, hız - zaman grafiğinin eğimi bize ivmeyi verir.

İvme - zaman grafiğinin altında kalan alan hızdaki değişimi, hız - zaman grafiğinin altında kalan alanda konumdaki değişimi (yer değiştirme) miktarını verir.

 

Hareket Örnek Soru:

Aralarında 200 m uzaklık bulunan K ve L hareketlileri birbirlerine doğru V_K = 5 m/s, V_L = 15 m/s sabit hızlarla aynı anda harekete başlamış olsunlar. K hareketlisi L ile karşılaştığında harekete geçtiği noktaya uzaklığı kaç metre olur?

 

Hareket Örnek Soru Çözümü:

Hızlar sabit, yani ivmeden söz edemiyoruz. bu yüzden bu arkadaşlar sabit hızlı hareket yapmış demektir.

K ve L hareketlileri aynı anda harekete geçip t süre sonra M noktasında karşılaşsınlar.
K’nın yerdeğiştirmesi x ise L ninki 200 – x olur.

Buna göre,

X = V.t olduğuna göre,

200 – x = 15t

x = 5 t dir.

200 – 5t = 15t den t = 10 s bulunur.

Yani hareketliler 10 saniye sonra karşılaşırlar. Bu sürede K hareketlisinin yerdeğiştirmesi

X_K = x = 5 . 10 = 50 m bulunur.

 Sonrakine devam edin... Düzgün hızlanan hareket

Soruların devamı:

Hareket Problemleri Çözümlü

 

Çıkmış Hareket Soruları

Hareket Resimleri Gif (animasyon)

 
Boyutu: 1.20 MB

Boyutu: 8.23 MB

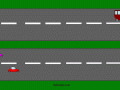
Boyutu: 241.67 Kb

Göktuğ S. Bozoklu / M.A (Fizik Öğretmeni)


Etiketler (ivme, hız, doğrusal, düzgün, sabit, düzlem, )
Tarafımızca yazılan yazıların hakları saklıdır.

Benzer Başlıklar... » Vektör nedir? » Kuvvet, keşişen kuvvetlerin dengesi » Deney , bağımlı , bağımsız ve sabit değişkenler » Skaler ve Vektörel Büyüklükler » Düzgün Doğrusal Hareket Grafikleri » Düzgün Hızlanan Hareket » Düzgün Yavaşlayan Hareket » Bir boyutta hareket » Hareket Nedir?

Yorumlar (3)3222

1. dem baba [10.04.2018, 09:14 ]

   ?

   bence siteniz güzel inanın bana ama bunu yazan insan nasıl acaba asdfawetsrhthsejö

Türkçemizi katletmeden harf ve imlâ yapımıza uyacağınızı düşünüyoruz.
Uygunsuz içerikler savcılığa bildirilmek üzere kayıt altına alıyoruz.
21.11.2024, 13:08

Adınız
Yorumunuz

Her hakkı saklıdır.
Görüntüleme 22535