PALANGALAR

Bir sistem düzeneğine hareketli ve sabit makara yerleştiriyoruz adına da palanga diyoruz. Yani hareketli ve sabit makaralardan oluşan sistemlerdir. Bolca vinçler üzerinde görürüz. İşlemleri oldukça basittir aslında. Bunu formül gibi değilde; eğer bir sistem dengede ise aşağı yönlü kuvvetler ile yukarı yönlü kuvvetler birbirine eşittir prensibini uygularsak daha rahat anlayabiliriz.

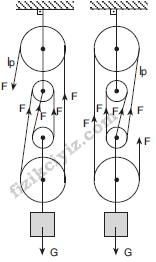
Şekil i          Şekil ii

 

Şekil (i) de G yükü dört ip tarafından dengelendiğinden

G = 4F  olur.

h: yükün yükselmesi

hkuvvet = hyük.4 olur. (ipin çekme/yükün yükselme miktari)

Şekil (ii) de G yükü beş ip tarafından dengelendiği için;

G = 5F dir.

h: yükselme miktari

hkuvvet = hyük.5 olur.(ipin çekme/yükün yükselme miktari)

• Makaralar ağırlıklı ise sadece hareketli makaranın ağırlıkları yüke eklenir

Görüldüğü gibi olay sadece yukarı yönlü kuvvetler ile aşağı yönlü kuvvetleri eşitlemek.

ÇIKRIK

 

Şekil i     Şekil ii

 

Şekil (i) kuyudan su çekmekte kullanılan çıkrığı, şekil (ii) ise bu çıkrığın yandan (profil) görünüşünü göstermektedir.

R = Kuvvet kolu (Çıkrık kolu)
r = Yük kolu (silindir yarıçapı)

Sistem dengede ise, O noktasına göre, yük ve kuvvetin momentleri eşit olmalıdır.

G.r = F.R

• R > r olduğundan, kuvvetten kazanç sağlanır. Yoldan kayıp olur.

• Yükün aldığı yol h;
h = Silindirin çevresi .n
n = Silindirin devir sayısı

 

EĞİK DÜZLEM

 

Şekildeki sürtünmesiz eğik düzlemde;

G: Cismin ağırlığı
F: Cismi eğik düzlemde hareket ettirmek için uygulanan kuvvet
l : Kuvvetin yolu
h: Yükün yolu.
Cisim dengede ise;

F = G.sinα = G. h/l

 F.l = G. h

l > h olduğu için kuvvetten kazanç vardır. Yoldan kayıp vardır.
• Yük l kadar ilerlerken h kadar da yükselir.

 

DİŞLİ ÇARKLAR

Hayataımızın her yerinde gördüğümüz çocukken merak edip baktığımız oyuncak arabalarda bolca kullanılan bu dişliler; dönme hızını ve dönme yönünü değiştiren araçlardır.

FARKLI EKSENLİ DİŞLİ ÇARKLAR

Şekildeki dişli çarklarda;

r1 ve r2: Çarkların yarıçapları
f1 ve f2 : Çarkların devir sayıları
d1 ve d2: Çarkların diş sayısı
ϑ1 ve ϑ2: Çarkların dönme hızı

Bu tür çarklarda

ϑ1 = ϑ2
f1 .r1 = f2.r2
f1.d1= f2.d2 dir.

∗ Birbirine değen çarklar zıt yönde dönerler.
∗ Yarıçapla, devir sayısı ters orantılıdır.
∗ Diş sayısıyla devir sayısı ters orantılıdır.
∗ Bir dişli üzerindeki diş sayısı yarıçapıyla doğru orantılıdır.

 

ORTAK EKSENLİ DİŞLİ ÇARKLAR

Merkezleri çakışacak biçimde perçinli dişlilerdir.

Diş sayıları, yarıçapları farklı olmasına rağmen, dönme yönleri ve devir sayıları eşittir.

Hızları farklıdır. Yarıçapı büyük olan dişlinin hızı da büyüktür. Yarıçapla doğru orantılıdır.

f1 = f2

ϑ1/ ϑ2 = r1 / r2

 

KASNAK

Yukarıdaki şekil (A) ve (B) kasnaklarını göstermektedir.

r1 ve r2 : Kasnakların yarıçapları
f1 ve f2 : kasnakların devir sayılarıdır.

f1r1 = f2r2 dir.

∗ Kasnaklar aynı yönde dönerler.
∗ Yarıçapla devir sayısı ters orantılıdır.

Kasnak yukardaki gibi olursa sadece yönler zıt olur. Yani kasnaklar zıt yönlü dönerler.

 

 

VİDA

F: Uygulanan kuvvet
r: kuvvet kolu
a: Vida adımı
R: Direnç kuvveti

Enerjinin korunumundan

F. 2π r = R. a dır.

Vidanin daire olan baş çevresini uygulanan kuvvet ile çarpımı ile tahtanın vidaya uyguladığı direç kuvveti ile vidanın adımının çarpına eşittir.

Kol (n) kez döndürüldüğünde vidanın tahtada ilerleme miktarı

h = n. a ile bulunur.

Son bir not edeyim; vidanın ilerleme miktarı h; F, R ve r ye bağlı değildir. ÖSYM'nin bu tür sorularına dikkat etmekte fayda var.

BÖLÜM I (Basit makine,nedir, ne işe yarar,kaldıraç ve türleri, makaralar (sabit ve hareketli))

Basit Makineler çözümlü sorular

ÖSS Basit Makinalar Çıkmış Sorular

GÖKTUĞ SERKAN BOZOKLU

Göktuğ S. Bozoklu / M.A (Fizik Öğretmeni)

Fotoğraflar (Sayfa 1)

Sayfalar o>>

Etiketler (palanga, çıkrık, dişli, kasnak, ve, vidalar, )
Tarafımızca yazılan yazıların hakları saklıdır.

Benzer Başlıklar... » Vektör nedir? » Kuvvet, keşişen kuvvetlerin dengesi » Deney , bağımlı , bağımsız ve sabit değişkenler » Skaler ve Vektörel Büyüklükler » Düzgün Doğrusal Hareket ve İvme » Basit Makineler; Nedir Ne işe yarar?, Kaldıraçlar,makaralar » Dengedeki bazı cisimler için şartlar, şemalar ve lami uygulanışı » Sıvılar basıncı II; u borusu, pistonlar, bileşik kaplar » Isı ve Isının yayılması

Yorumlar (6)3102

1. beyza [14.11.2017, 20:11 ]

   ?

   Süper bayildim

2. Onur [17.12.2018, 22:17 ]

   ?

   Emekleriniz için teşekkürler.

3. Deniz Kumlu [03.03.2019, 14:42 ]

   ?

   T eş ekkurler elinize saglik

4. Deniz Kumlu [10.07.2019, 17:27 ]

   ?

   SORU SORABİLİRMİYİM

Türkçemizi katletmeden harf ve imlâ yapımıza uyacağınızı düşünüyoruz.
Uygunsuz içerikler savcılığa bildirilmek üzere kayıt altına alıyoruz.
21.11.2024, 15:28

Adınız
Yorumunuz

Her hakkı saklıdır.
Görüntüleme 78638